• Плоскі кривіі. Криві другого порядку
• Просторові криві лінії
• Криві поверхні. Способи їх утворення

     Криві поверхні широко застосовуються в різних галузях машинобудування, будівництва тощо. Поверхня вважається заданою, якщо відносно будь-якої точки простору можна вирішити питання щодо її належності даній поверхні.

Залежно від способу утворення одну й ту ж поверхню можна віднести до таких класів: кінематична – утворена рухом твірної по напрямних або каркасна – наближено представлена ліній ним чи точковим каркасом.

Найбільш поширені поверхні, утворені за кінематичним законом з твірними постійної форми (лінійчаті та нелінійчаті).

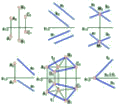
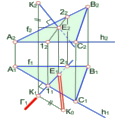
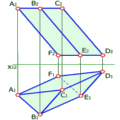
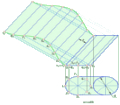
Лінійчатою називають поверхню, яка може бути утворена рухом прямої лінії за певним законом. До них відносять: циліндричні, конічні, гвинтові тощо. На рис. 7.9 побудовано торс (лінійчата циліндрична поверхня), що має назву розгортуваного гелікоїда. Ребром звороту його є геліса. Твірна гелікоїда перекочується по гвинтовій лінії, залишаючись дотичною до неї. Для побудови геліси коло в плані та циліндр по висоті розділено на 8 рівних частин. Спочатку побудована твірна гелікоїда, яка проходить через точку 3, вона паралельна до фронтальної площини проекцій. Визначена точка перетину цієї кривої з площиною П1. Горизонтальна проекція дотичної має назву піддотичної. Дотичні до геліси утворюють однакові кути з П1 . тому розмір піддотичної в точці 2, що знаходиться на рівні 1/8 висоти циліндра, вдвічі менший за піддотичну в точці 3, яка розміщена на рівні 2/8 висоти циліндра. Приймаючи розмір піддотичної в точці 2 за одиницю, відкладаємо на полі П1 на дотичній в точці 4 три таких відрізки, в точці 5 – чотири і т.д. На фронтальній проекції вони знаходяться за відповідністю з горизонтальною проекцією. Горизонтальні сліди твірних визначить горизонтальний слід поверхні у вигляді кривої, яка є евольвентною кола.

Рис. 7.9

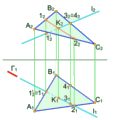
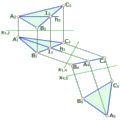
     Якщо поверхня розгортається, то вона є розгортуваною (циліндр, конус) (рис. 7.10), а якщо не розгортається – нерозгортуваною (гіперболічний параболоїд), лінійчатий (однопорожнинний) гіперболоїд тощо (рис. 7.11).

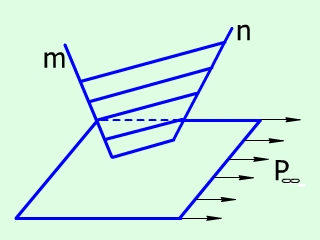
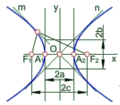
     Гіперболічний параболоїд – це поверхня, що має 2-й алгебраїчний порядок, визначником, якої є дві мимобіжні прямі m і n та горизонтальна площина паралелізму Р.

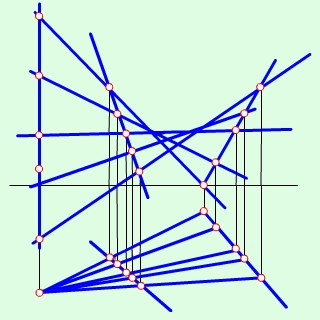
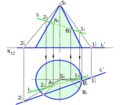
Лінійчастий гіперболоїд утворюється при русі прямої твірної по трьох мимобіжних напрямних – а, в, с. Для полегшення побудови одну з прямих (а) взято у вертикальному положенні, це дає змогу безпосередньо проводити прямі твірні. Побудову прямих виконано спочатку на горизонтальній проекції. Проведено серію твірних, і визначено точки перетину цих твірних з напрямними в та с. За відповідністю знаходяться фронтальні проекції твірних.

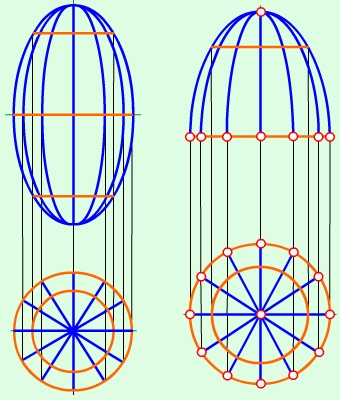
В різних галузях техніки широко застосовуються поверхні з постійною криволінійною твірною, з них можна виділити поверхні обертання. Точки твірної описують навколо осі кола, які називаються паралелями, а криві, одержані в результаті перетину поверхні обертання площинами, що проходять через вісь, називають меридіанами. Паралелі та меридіани утворюють на поверхні обертання ортогональну сітку. Якщо вісь обертання проходить через центр твірного кола, при його обертанні матимемо сферу або ж еліпсоїд обертання (рис.4.18, а). На рис.4.1,б представлено параболоїд обертання.

• Перелік тем